Today I would like to share my fascination with Artificial Intelligence (AI) by explaining what their fundamental building blocks are:
It is known to all that computer programming is ultimately translated to a group of 1s and 0s for certain instructions to be executed. We are able to utilise various techniques to execute instructions, programming languages.
Each programming language comes with its own pros and cons, but this post is not about comparing them (I will maybe save that for another time). The truth is, most languages differ in syntax. Amidst varying lines of code and legibility, one thing does not change: The end result.
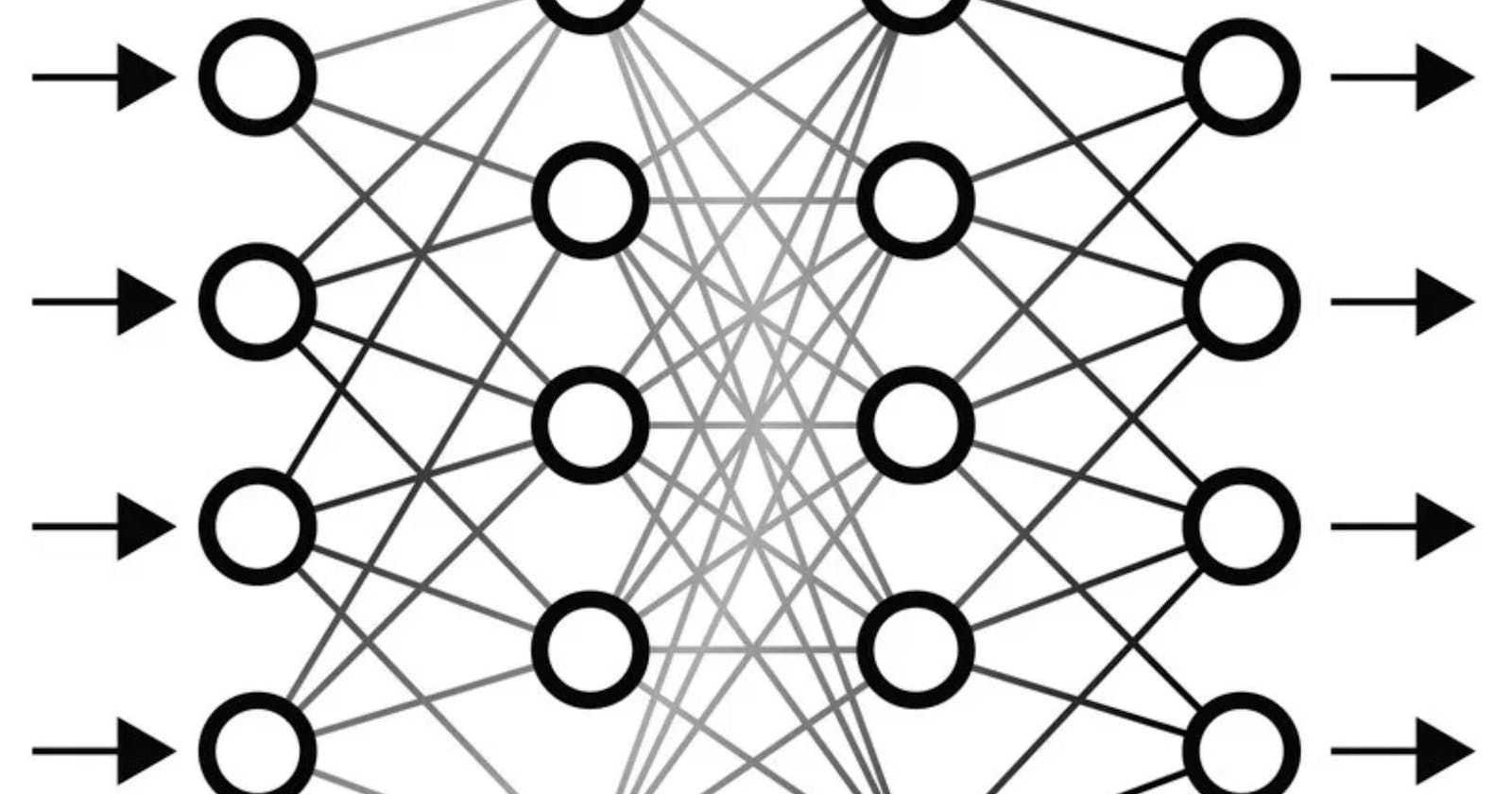
I find it really interesting that apart from translating syntax to machine code, we can even manage to write advanced algorithms and create an approach where the program adapts and predicts on the go. I am thinking of Artificial Neural Networks (ANNs).
Each neurone in the network has a so-called "activation function" of its own, which is essentially a statistical function borrowed from Mathematics. The very popular activation function 'ReLU' stands for 'Rectified Linear Unit' which outputs a 0 for any input less than 0. Now one neurone cannot achieve much because there is only one function that is consists of. This is exactly why we have a network.
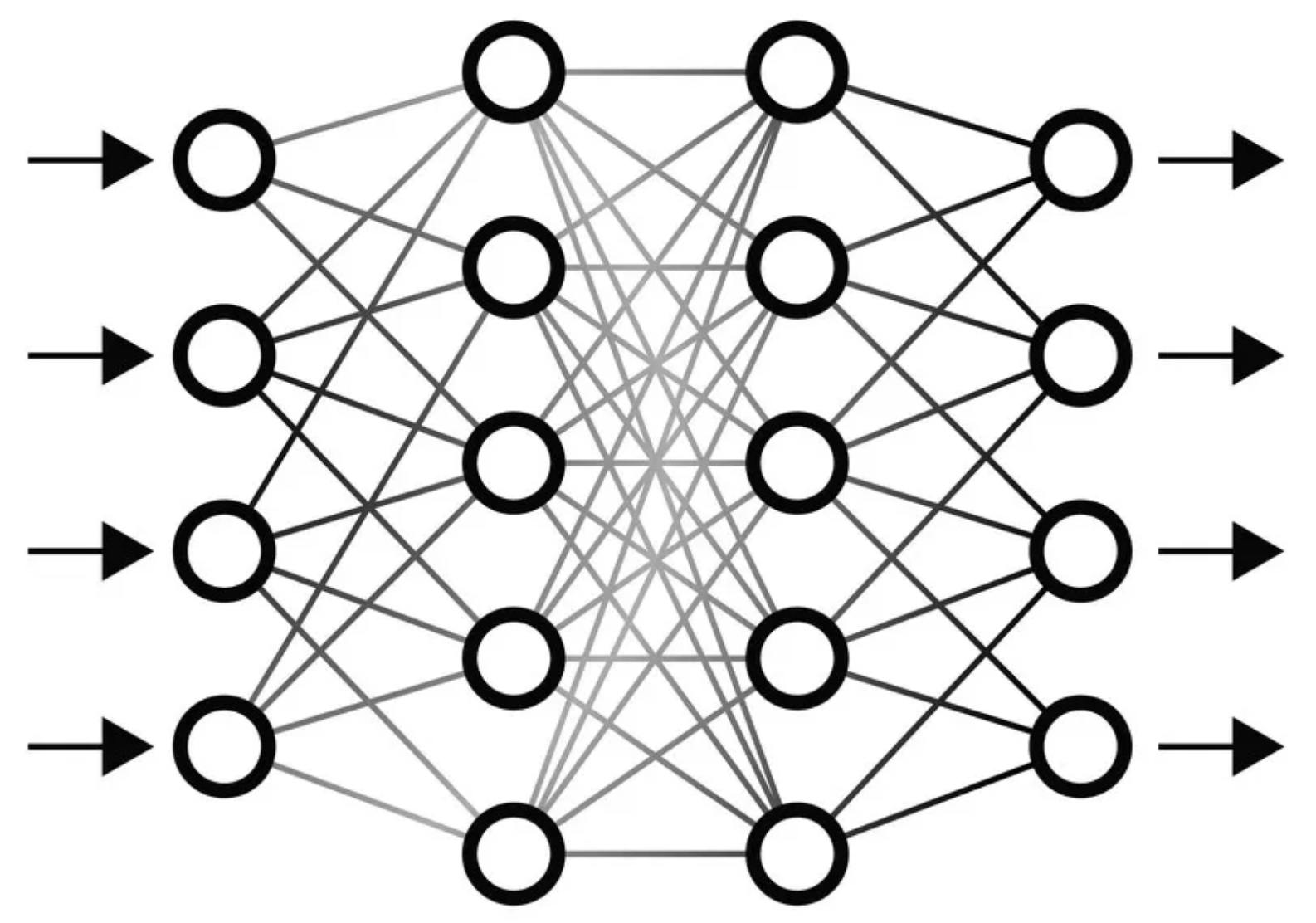
Before the input is fed to the network, it is first linearised (A Math spy has been spotted). By linearising, we mean that the output of the linearisation layer or commonly-known as "input layer" is in the form of WX+B. (A refresher to your high school Math, the linear formula outputs a straight line when visualised). The "W" in the formula are called the "weights" of our input while "B" stands for "bias". We will discuss further on weights as we go over the Math.
Y = WX + B
Creating a network of interconnected neurones means that the output of each neurone becomes the input of every neurone in the next layer of the network. If given some thought, it is evident that every layer's output is constantly refined as the input is iterated through the network. What does this mean? Well, the program can capture the pattern in the input and guess what comes next in the sequence, assuming our input to the network is a sequence of numbers (A Matrix, Vector or Tensor).
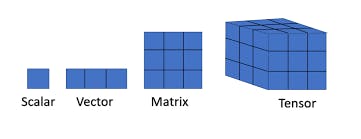
You might ask me, "If all the Math that's being used is just statistics, is it really a game-changer?". There's actually much in store for us. Not only does our input get refined over iterations through the network, but is also adjusted when the network compares what it's predicting with the true value provided by us. This is called "backpropagation".
Backpropagation uses Calculus, which is my favourite concept in Math. The algorithm first finds the differential of output and checks how close the result is to zero. The closer it is to zero, the more accurate the predictions. You can think of the differential as a cost, which means lesser is better.
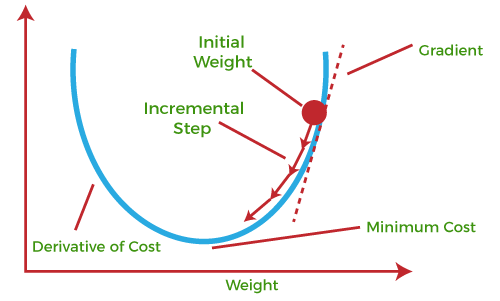
Weights are usually randomly initialised and are optimised as we iterate through the network. They are optimised using backpropagation. This algorithm essentially tweaks the weights such that the pattern captured by the network is similar, if not same, to the actual value provided by a human.
Usually, the optimisation of the network is done until the set number of iterations. The input's pattern is captured with the best of the ANNs abilities only until we ask it to do. Overall there is a LOT more to AI than ANNs, but they are a start that leads to Deep Learning.